The Neural Nexus: Unraveling the Power of Activation Functions in Neural Networks

In the realm of neural networks, one of the most crucial yet often overlooked components is the activation function. As the "neural switch," activation functions play a fundamental role in shaping the output of individual neurons and, by extension, the overall behavior and effectiveness of the network. They are the key to introducing nonlinearity into neural networks, enabling them to model complex relationships in data and solve a wide range of real-world problems. In this comprehensive article, we delve deep into the fascinating world of activation functions, exploring their significance, various types, and the impact they have on training and performance. By understanding the neural nexus, we gain valuable insights into the art and science of designing powerful neural networks that fuel the advancement of artificial intelligence.

The Foundation of Activation Functions

At the core of every neural network, artificial neurons process incoming information and produce an output signal. The output of a neuron is determined by applying an activation function to the weighted sum of its inputs and biases. This process mimics the firing behavior of biological neurons in the brain, where the neuron activates or remains inactive based on the input signal's strength.

The Role of Nonlinearity

The key role of activation functions lies in introducing nonlinearity into the neural network. Without nonlinearity, the network would be reduced to a series of linear transformations, incapable of modeling complex patterns in data. Nonlinear activation functions enable the composition of multiple non-linear functions, allowing the network to approximate highly intricate mappings between inputs and outputs. As a result, neural networks become capable of solving a wide range of problems, from image recognition and natural language processing to medical diagnosis and financial prediction.

The Landscape of Activation Functions

This section explores various types of activation functions that have been developed over the years. We start with the classic step function, which was one of the earliest activation functions used. However, due to its discontinuity and lack of differentiability, the step function is rarely used in modern neural networks.

Next, we delve into the widely-used Sigmoid function. The Sigmoid function maps the entire input range to a smooth S-shaped curve, effectively squashing large positive and negative inputs to the range (0, 1). While the Sigmoid function provides nonlinearity, it suffers from the vanishing gradient problem. As the output approaches the extremes (0 or 1), the gradient becomes extremely small, leading to slow learning or getting stuck in training.

The Hyperbolic Tangent (TanH) function is another popular activation function that addresses the vanishing gradient issue of the Sigmoid. The TanH function maps the input range to (-1, 1), allowing for stronger gradients and faster learning. However, TanH still suffers from the vanishing gradient problem, particularly for large inputs.

The Rectified Linear Unit (ReLU) is one of the most widely used activation functions in modern neural networks. ReLU maps the input to zero for negative values and leaves positive values unchanged. ReLU effectively solves the vanishing gradient problem for positive inputs, as its gradient is 1 for positive values, enabling faster convergence. However, ReLU can suffer from the "dying ReLU" problem, where neurons can become inactive and never recover from negative inputs.

To mitigate the issues of ReLU, researchers introduced variants like Leaky ReLU and Parametric ReLU. Leaky ReLU introduces a small, non-zero slope for negative inputs, preventing neurons from becoming inactive. Parametric ReLU takes this a step further by allowing the slope to be learned during training, making it more adaptive to the data.

Advanced activation functions like Exponential Linear Units (ELUs) and Swish have been proposed to improve on the drawbacks of ReLU. ELUs introduce smoothness to the function, preventing the "dying ReLU" problem and providing faster convergence. Swish combines the simplicity of ReLU with a smooth S-shaped curve, offering better performance on certain tasks.

Activation Functions in Action - Coding Examples

To grasp the practical implications of activation functions, let's look at coding examples demonstrating how they affect neural network behavior. We will use Python and the popular deep learning library TensorFlow/Keras for implementation. We'll create a simple neural network with one hidden layer and experiment with different activation functions.

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

# Generate sample data
X = np.linspace(-5, 5, 1000).reshape(-1, 1)

# Create a neural network model with one hidden layer
model = tf.keras.Sequential([
    tf.keras.layers.Dense(64, activation='linear', input_shape=(1,)),
    tf.keras.layers.Activation('relu'),
    tf.keras.layers.Dense(1, activation='linear')
])

# Compile the model with an appropriate optimizer and loss function
model.compile(optimizer='adam', loss='mse')

# Train the model
history_relu = model.fit(X, X, epochs=1000, verbose=0)

# Change activation function to Swish
model.layers[1].activation = tf.keras.activations.swish

# Recompile the model
model.compile(optimizer='adam', loss='mse')

# Train the model with Swish
history_swish = model.fit(X, X, epochs=1000, verbose=0)

# Plot the training loss for both ReLU and Swish
plt.plot(history_relu.history['loss'], label='ReLU')
plt.plot(history_swish.history['loss'], label='Swish')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Comparison of ReLU and Swish Activation Functions')
plt.legend()
plt.show()

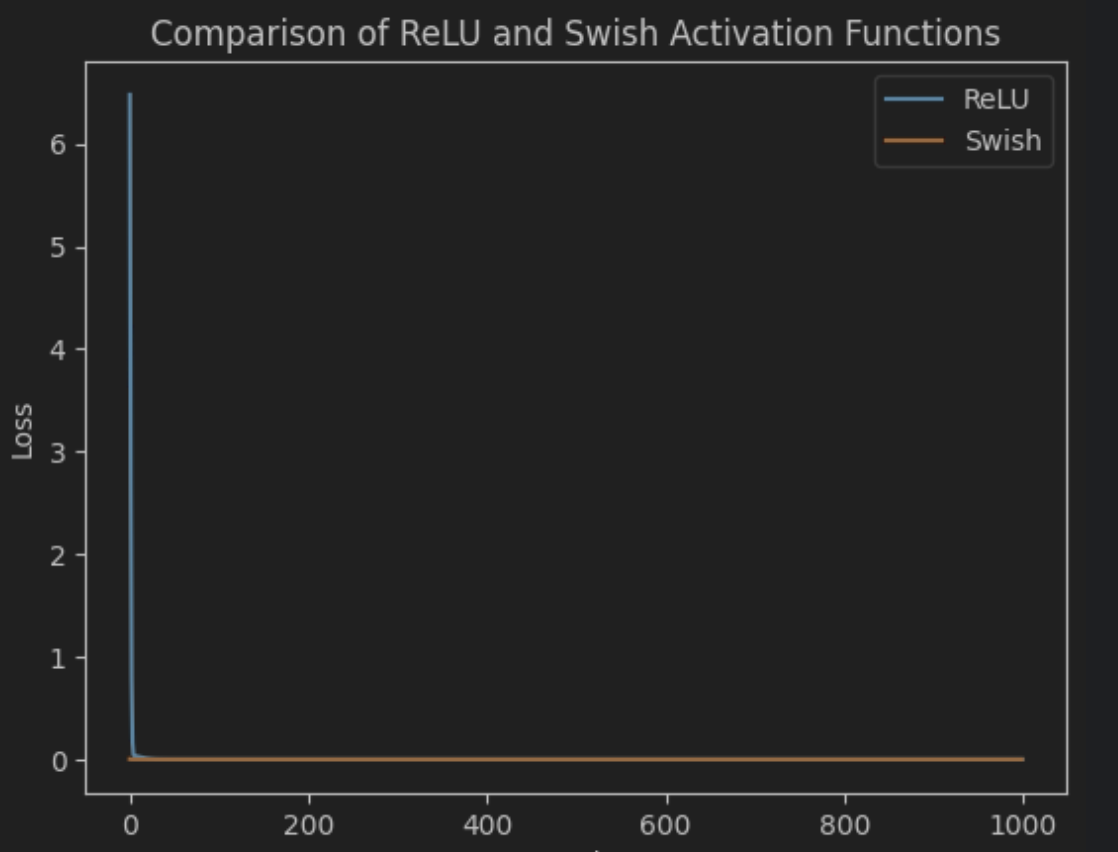
In this example, we compare the training loss of a neural network using ReLU and Swish activation functions. We observe how Swish converges faster and achieves a lower loss compared to ReLU.

The Impact on Training and Performance

Different activation functions significantly affect the training dynamics of neural networks. The choice of activation function impacts the network's convergence speed, gradient flow, and ability to handle vanishing or exploding gradients.

In the coding example above, we observed how Swish outperformed ReLU in terms of convergence speed and loss. While both activation functions achieved good results, Swish exhibited better behavior during training.

To gain a deeper understanding, we can create additional experiments to compare the performance of activation functions on different tasks and architectures. For instance, some activation functions may perform better on image classification tasks, while others excel in natural language processing tasks.

Adaptive Activation Functions

To address some limitations of traditional activation functions, researchers have explored adaptive approaches. The Swish activation function, for example, is a hybrid of ReLU and the Sigmoid function, and it automatically adapts to the characteristics of the data.

Another adaptive activation function is the Adaptive Piecewise Linear (APL) activation. This function learns the slope and intercept of each activation during training, allowing for better adaptability to different data distributions.

These adaptive activation functions aim to strike a balance between computation efficiency, gradient behavior, and performance on diverse tasks, making them valuable additions to the arsenal of activation functions.

Activation Functions in Advanced Architectures

Activation functions play a pivotal role in more advanced architectures like residual networks (ResNets) and transformers. In residual networks, the identity shortcut connections are particularly effective in mitigating the vanishing gradient problem, enabling deeper and more efficient networks. Such architectures leverage activation functions to maintain gradient flow across layers and ensure smooth training.

In transformers, the self-attention mechanism enables capturing long-range dependencies in data. Activation functions in transformers contribute to modeling the interactions between different tokens in the input sequence, allowing the network to excel in natural language processing tasks.

The Quest for the Ideal Activation Function

While the field of activation functions has witnessed significant progress, the quest for the ideal activation function continues. Researchers are constantly exploring new activation functions, aiming to strike a balance between computation efficiency, gradient behavior, and performance on diverse tasks.

The ideal activation function should be able to alleviate the vanishing gradient problem, promote faster convergence, and handle a wide range of data distributions. Additionally, it should be computationally efficient and avoid issues like the "dying ReLU" problem.

The choice of activation function is also heavily influenced by the network architecture and the specific task at hand. Different activation functions may perform better or worse depending on the complexity of the problem and the data distribution.

Comparison Summary

To summarize the comparison of various activation functions:

1. Sigmoid and TanH functions: Both suffer from the vanishing gradient problem, making them less suitable for deep networks. They are rarely used as hidden layer activations in modern networks.
2. ReLU and its variants (Leaky ReLU, Parametric ReLU): ReLU is widely used due to its simplicity and faster convergence for positive inputs. Leaky ReLU and Parametric ReLU variants aim to address the "dying ReLU" problem and achieve better performance in certain scenarios.
3. ELU and Swish functions: ELU introduces smoothness and avoids the "dying ReLU" problem, while Swish combines the simplicity of ReLU with better performance.
4. Adaptive activation functions (Swish and APL): These functions automatically adapt to the data, making them suitable for a wide range of tasks and data distributions.

Conclusion

Activation functions are the unsung heroes of neural networks, wielding immense influence over the learning process and network behavior. By introducing nonlinearity, these functions enable neural networks to tackle complex problems and make remarkable strides in the field of artificial intelligence. Understanding the nuances and implications of different activation functions empowers researchers and engineers to design more robust and efficient neural networks, propelling us ever closer to unlocking the full potential of AI and its transformative impact on society. As the quest for the ideal activation function continues, the neural nexus will continue to evolve, driving the progress of artificial intelligence toward new frontiers and uncharted territories.